6章 学習に関するテクニック

準備

library(tidyverse)
library(R6)

source("common/functions.R")

パラメータの更新

SGD

SGD <- R6Class("SGD", list(
  lr = NULL,
  initialize = function(lr = 0.01) {
    self$lr <- lr
  },
  update = function(params, grads) {
    for (name in names(grads)) {
      params[[name]] <- params[[name]] - self$lr * grads[[name]]
    }
    params
  }))

Momentum

Momentum <- R6Class("Momentum", list(
  lr = NULL,
  momentum = NULL,
  v = NULL,
  initialize = function(lr = 0.01, momentum = 0.9) {
    self$lr <- lr
    self$momentum <- momentum
  },
  update = function(params, grads) {
    if (is.null(self$v)) {
      self$v <- map(params, ~ 0)
    }
    for (name in names(params)) {
      self$v[[name]] <- self$momentum * self$v[[name]] - self$lr * grads[[name]]
      params[[name]] <- params[[name]] + self$v[[name]]
    }
    params
  }))

AdaGrad

AdaGrad <- R6Class("AdaGrad", list(
  lr = NULL,
  h = NULL,
  initialize = function(lr = 0.01) {
    self$lr <- lr
  },
  update = function(params, grads) {
    if (is.null(self$h)) {
      self$h <- map(params, ~ 0)
    }
    for (name in names(params)) {
      self$h[[name]] <- self$h[[name]] + grads[[name]] ^ 2
      params[[name]] <- params[[name]] - self$lr * grads[[name]] / (sqrt(self$h[[name]]) + 1e-7)
    }
    params
  }))

Adam

Adam <- R6Class("Adam", list(
  lr = NULL,
  beta1 = NULL,
  beta2 = NULL,
  iter = NULL,
  m = NULL,
  v = NULL,
  initialize = function(lr = 0.001, beta1 = 0.9, beta2 = 0.999) {
    self$lr <- lr
    self$beta1 <- beta1
    self$beta2 <- beta2
    self$iter <- 0
  },
  update = function(params, grads) {
    if (is.null(self$m)) {
      self$m <- map(params, ~ 0)
      self$v <- map(params, ~ 0)
    }
    self$iter <- self$iter + 1
    lr_t <- self$lr * sqrt(1 - self$beta2 ^ self$iter) / (1 - self$beta1 ^ self$iter)
    for (name in names(params)) {
      self$m[[name]] <- self$m[[name]] + (1 - self$beta1) * (grads[[name]] - self$m[[name]])
      self$v[[name]] <- self$v[[name]] + (1 - self$beta2) * (grads[[name]]^2 - self$v[[name]])
      params[[name]] <- params[[name]] - lr_t * self$m[[name]] / (sqrt(self$v[[name]]) + 1e-7)
    }
    params
  }))

どの更新手法を用いるか？

f <- function(x, y) x^2 / 20 + y^2
df <- function(x, y) list(x / 10, 2 * y)

init_pos <- list(x = -7.0, y = 2.0)
params <- init_pos

optimizers <- list(
  SGD = SGD$new(lr = 0.95),
  Momentum = Momentum$new(lr = 0.1),
  AdaGrad = AdaGrad$new(lr = 1.5),
  Adam = Adam$new(lr = 0.3)
)

update <- function(optimizer, init_pos, n = 30) {
  params <- init_pos
  map_dfr(1:n, function(i) {
    grads <- df(params$x, params$y) %>%
      set_names(c("x", "y"))
    params <<- optimizer$update(params, grads)
  }) %>%
    rbind(init_pos, .)
}

results <- map(optimizers, update, init_pos)

results %>%
  imap_dfr(~ mutate(.x, optimizer = .y)) %>%
  mutate(optimizer = factor(optimizer, levels = names(optimizers))) %>%
  ggplot(aes(x, y)) +
  geom_line() +
  facet_wrap(vars(optimizer), nrow = 2)

重みの初期値

隠れ層のアクティベーション分布

node_num <- 100
hidden_layer_size <- 5
n <- 1000

set.seed(1)
x1 <- matrix(rnorm(n * node_num), n, node_num)

accum_activations <- function(init, activation = sigmoid) {
  accumulate(
    1:hidden_layer_size,
    function(x, i) {
      w <- matrix(rnorm(node_num * node_num), node_num) * init
      a <- x %*% w
      activation(a)
    },
    .init = x1
  ) %>% tail(-1)
}

plot_activations <- function(activations) {
  activation_df <- activations %>%
    imap_dfr(~ tibble(layer = .y, a = as.vector(.x)))

  ggplot(activation_df, aes(x = a)) +
    geom_histogram(binwidth = 0.02) +
    coord_cartesian(xlim = c(0, 1)) +
    facet_wrap(vars(layer), nrow = 1)
}

0と1に偏ったデータ分布

activations <- accum_activations(1)
plot_activations(activations)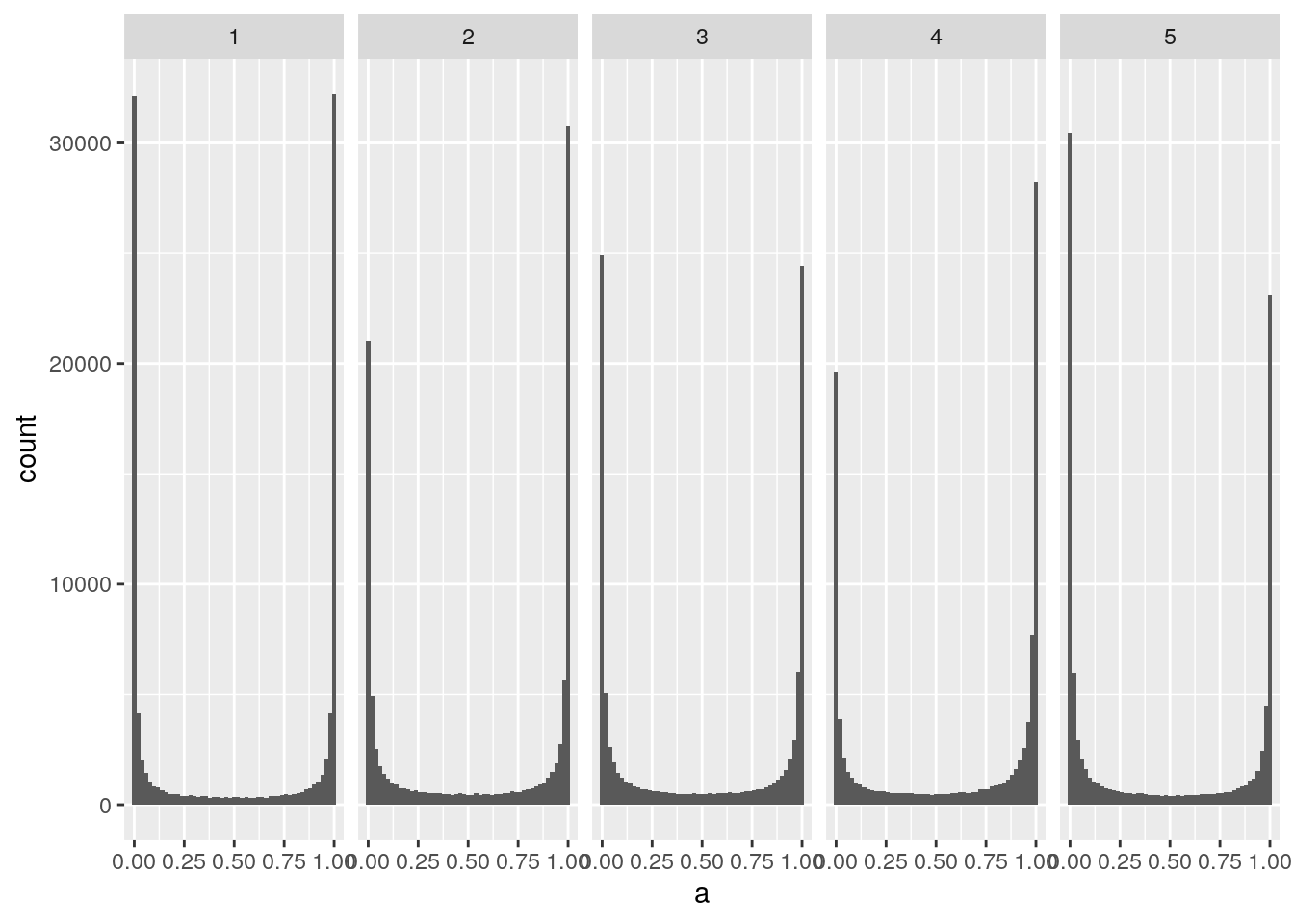

重みの標準偏差を0.01にする。

activations <- accum_activations(0.01)
plot_activations(activations)

Xavierの初期値を使う。

activations <- accum_activations(sqrt(1 / node_num))
plot_activations(activations)

ReLUの場合の重みの初期値

relu <- function(x) ifelse(x > 0, x, 0)

標準偏差が0.01のガウス分布を重みの初期値とした場合

activations <- accum_activations(0.01, relu)
plot_activations(activations)

Xavierの初期値の場合

activations <- accum_activations(sqrt(1 / node_num), relu)
plot_activations(activations)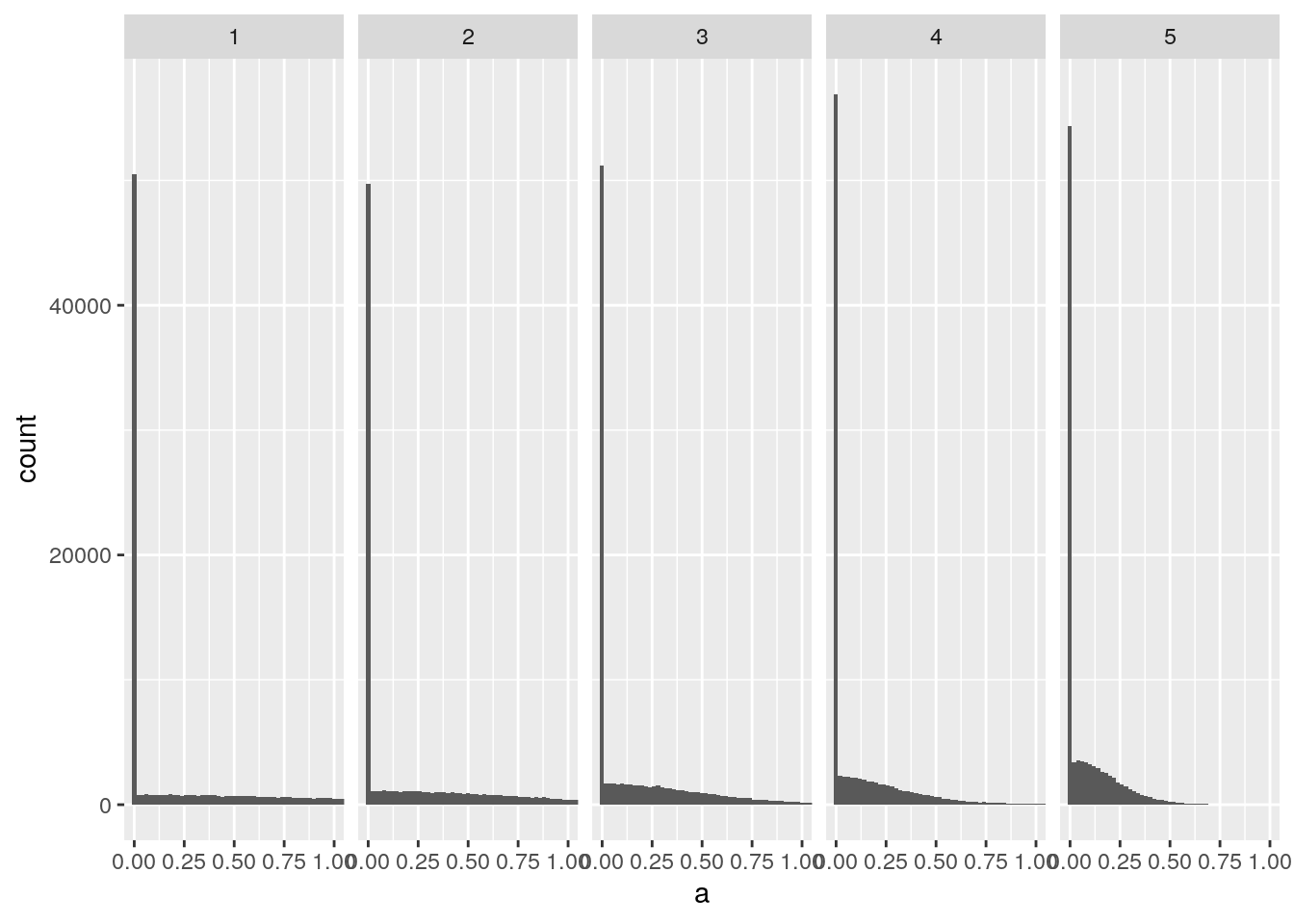

Heの初期値の場合

activations <- accum_activations(sqrt(2 / node_num), relu)
plot_activations(activations)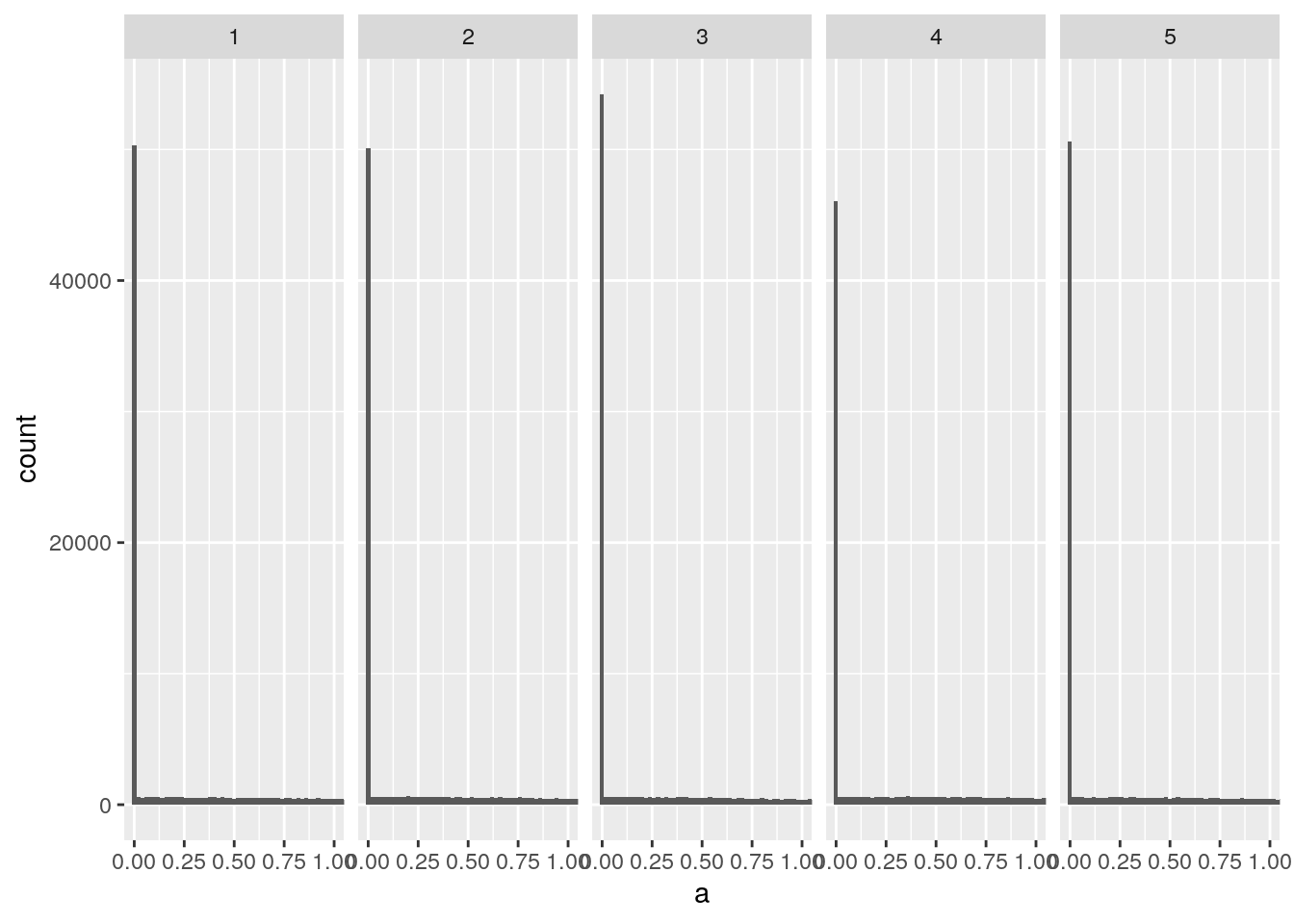

Batch Normalization

TODO

正則化

TODO

ハイパーパラメータの検証

TODO